MATEMÀTICAS
Se conoce como matemática o matemáticas, según corresponda a la costumbre, al estudio de todas aquellas propiedades y relaciones que involucran a los entes abstractos, como ser los números y figuras geométricas, a través de notaciones básicas exactas y del razonamiento lógico.

Como todo estudio, las matemáticas surgieron como consecuencia de algunas necesidades que el hombre comenzó a experimentar, entre ellas, hacer los cálculos inherentes a la actividad comercial y por supuesto, hacerlos bien para que la misma pudiese seguir existiendo, para medir la tierra y para poder predecir algunos fenómenos astronómicos. Mucha gente supone que estas carencias fueron las que provocaron la subdivisión actual de las matemáticas, en estudio de la cantidad, estructura, cambio y espacio.
La mayoría de los objetos de estudio de las matemáticas, los números, la geometría, los problemas, el análisis, son todas cuestiones que seamos o no seamos estudiosos o fanáticos de la materia debemos conocer porque de alguna u otra manera se relacionan con nuestra actividad cotidiana, aún cuando nuestra profesión o quehacer esté bien alejado de la resolución de problemas matemáticos. Por ejemplo, para una ama de casa, es sumamente importante tener nociones matemáticas para resolver o decidir compras en el supermercado, entre otros.
Asimismo, para lograr una correcta descripción, análisis y predicción de algunos fenómenos es necesaria la matemática, que nos ayudará con estas cuestiones a través de ramas como la probabilidad y la estadística tan funcionales cuando de estos temas se trata.
Números naturales
Se llaman números naturales a aquellos números que se pueden obtener al sumar el número 1 a sí mismo la cantidad de veces que se quiera. Así, tendríamos que el dos es un número natural pues 2=1+1, tres también lo es pues 3=1+1+1=2+1, cuatro también 4=1+1+1+1=3+1=2+2, y así sucesivamente.El conjunto que se va formando no tiene un último elemento, es decir, es infinito. Es fácil demostrarlo: Supongamos que n es el último número natural que podemos tener. Siempre se le puede sumar 1 a cualquier número natural y obtendremos un natural, por lo tanto (n+1) existe y es un número natural. Entonces n no era el último, (n+1) debe serlo. Entonces razonamos de igual forma para (n+1)y así sucesivamente. Esta argumentación no tiene fin: entonces no existe un último número natural, con lo cual el conjunto es infinito.
Números enteros
Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, ...), los opuestos de los números naturales (..., −3, −2, −1) y al cero, 0.El conjunto de todos los números enteros se representa por la letra ℤ = {..., −3, −2, −1, 0, +1, +2, +3, ...}, que proviene del alemán Zahlen («números», pronunciado [ˈtsaːlən]).
Los números enteros se pueden subdividir en dos categorías, los Pares y los Impares.
Números Pares
Los números enteros se pueden subdividir en dos categorías, una de ellas, la de los números pares está formada por los números enteros múltiplos de 2, es decir, un número entero m es número par si y solo si existe otro número entero n tal que: m = 2 x n. La cifra final de los números pares puede ser: 0, 2, 4, 6 u 8.
Números Impares
Los números enteros se pueden subdividir en dos categorías, una de ellas, la de los números impares está formada por los números enteros que no son múltiplos de 2, es decir, un número entero m es número impar si y solo si existe otro número entero n tal que: m = 1 + 2 x n.Los números impares siempre terminan con un dígito 1,3,5,7, o 9. Así que 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31 son números impares.
Matemáticas/Aritmética/Números racionales
En sentido amplio, se llama número racional a todo número que puede representarse como el conciente de dos enteros con denominador distinto de cero (una fracción común). El término racional alude a ración o parte de un todo, y no al pensamiento o actitud racional.En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de todas ellas, se toma como representante cònicode dicho número racional a la fracciòn irreducible, la de términos más sencillos.
Definimos un número racional como un decimal finito o infinito periódico (por ejemplo, el número decimal finito 0,75 es la representación decimal del número racional 3/4. El número decimal infinito periódico 0,333... es la representación decimal del número racional 1/3). El número racional permite resolver ecuaciones del tipo ax = b, cuando a y b son números enteros (con «a» distinto de cero).
El conjunto de los números racionales se denota por
 , que significa «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los nùmeros enteros y es un subconjunto de los números reales. Las fracciones equivalentes entre sí –número racional– son una clase de equivalencia, resultado de la aplicación de una relaciòn de equivalencia al conjunto denúmeros fraccionarios.
, que significa «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los nùmeros enteros y es un subconjunto de los números reales. Las fracciones equivalentes entre sí –número racional– son una clase de equivalencia, resultado de la aplicación de una relaciòn de equivalencia al conjunto denúmeros fraccionarios.Los números racionales cumplen la propiedad arquimediana o de densidad, esto es, para cualquier pareja de números racionales existe otro número racional situado entre ellos, propiedad que no estaba presente en los números enteros, por lo que los números racionales son densos en la recta de los números reales.
Historia
En el Antiguo Egipto ya se calculaba utilizando aquéllas cuyos denominadores son enteros positivos, como: cualquier fracción que escribimos con un numerador no unitario, los egipcios la escribían como suma de fracciones unitarias distintas, de ahí que las sumas de fracciones unitarias se conozcan como fracción egipcia. Además, se puede demostrar que cualquier número racional positivo se puede escribir como fracción egipcia.El jeografico de una boca abierta (
|
|} Los babilónicos utilizaban fracciones cuyo denominador era una potencia de 60, mientras que los egipcios usaron, sobre todo, las fracciones con numerador igual a 1. En la escritura, la fracción la expresaban con un óvalo, que significaba parte o partido, y debajo, o al lado, ponían el denominador; el numerador no se ponía por ser siempre 1.
Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval.
En el siglo XIII Leonardo de Pisa, mejor conocido como Fibonacci, introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.
Construcción de los números racionales
- Consideremos las parejas de números enteros
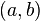 donde
donde 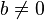 .
.
 denota a
denota a 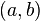 . A
. A  se le llama numerador y a
se le llama numerador y a  se le llama denominador
se le llama denominador
- Al conjunto de estos números se le denota por
 . Es decir
. Es decir 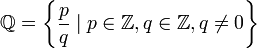
Definición de suma y multiplicación en Q
- Se define la suma

- Se define la multiplicación

Relaciones de equivalencia y orden en Q
- Se define la equivalencia
 cuando
cuando 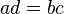
- Los racionales positivos son todos los
 tales que
tales que 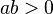
- Los racionales negativos son todos los
 tales que
tales que 
- Se define el orden
 cuando
cuando 
Notación
- Los números de tipo
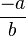 son denotados por
son denotados por 
- Las sumas de tipo
 son denotadas por
son denotadas por 
 denota a
denota a 
- Todo número
 se denota simplemente por
se denota simplemente por  .
.Unicidad de un racional
Un número racional sólo puede provenir de una única fracción irreducible.Propiedades de los números racionales
El conjunto de los números racionales con la suma y multiplicación definida de esta manera forman un Cuerpo.Propiedades de la suma y multiplicación
- La suma en Q es conmutativa, esto es:

- La suma en Q es asociativa, esto es:
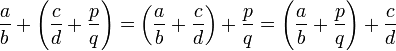
- La multiplicación en Q es asociativa, esto es:

- La multiplicación se distribuye en la suma, esto es

Existencia de neutros e inversos
- Para cualquier número racional:
 se cumple que
se cumple que 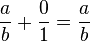 entonces
entonces  es el neutro aditivo de los racionales y se le denota por
es el neutro aditivo de los racionales y se le denota por  .
. - Para cualquier número racional:
 se cumple que
se cumple que 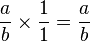 entonces
entonces  es el neutro multiplicativo de los racionales y se le denota por
es el neutro multiplicativo de los racionales y se le denota por  .
. - Cada número racional:
 tiene un inverso aditivo
tiene un inverso aditivo 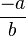 tal que
tal que 
- Cada número racional:
 con excepción de
con excepción de  tiene un inverso multiplicativo
tiene un inverso multiplicativo  tal que
tal que 
Equivalencias notables en Q
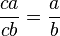 si
si  y
y 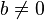
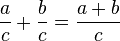

 , a y b ≠ 0
, a y b ≠ 0 , a y b ≠ 0.
, a y b ≠ 0.Los números enteros en Q
- Si
 es un número entero entonces existe el número
es un número entero entonces existe el número  que equivale a
que equivale a  y mantiene todas sus propiedades de entero. Es decir, se define
y mantiene todas sus propiedades de entero. Es decir, se define 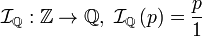
Otras notaciones de números en Q
Fracciones mixtas
Cada número racional se puede expresar de forma única como
se puede expresar de forma única como  donde
donde
- A es un entero no negativo, es decir
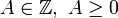
 es un racional irreducible no negativo menor que uno. Se expresa como
es un racional irreducible no negativo menor que uno. Se expresa como 
 es una unidad. Es decir
es una unidad. Es decir 
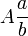 denota a
denota a 
 denota a
denota a 

El conjunto de los números decimales en Q
- Un número decimal es un número racional de la forma

 denota al conjunto de los números de este tipo. Es decir
denota al conjunto de los números de este tipo. Es decir 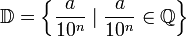
- Expresión Racional de un número decimal: el número
 en base
en base  con un punto a
con un punto a  lugares del extremo derecho, por ejemplo
lugares del extremo derecho, por ejemplo  se denota como
se denota como 
Representación decimal de los números racionales
Los números racionales se caracterizan por tener un desarrollo decimal cuya expresión sólo puede ser de tres tipos:
- Exacta: la parte decimal tiene un número finito de cifras. Ejemplo:
- Periódica pura: toda la parte decimal se repite indefinidamente. Ejemplo:
- Periódica mixta: no toda la parte decimal se repite. Ejemplo:
- Decimales exactos o finitos: Se escribe en el numerador la
expresión decimal sin la coma (como un número entero), y en el
denominador un uno seguido de tantos ceros como cifras decimales.
Ejemplo:

- Decimales periódicos puros: La fracción de un número decimal
periódico tiene como numerador la diferencia entre el número escrito sin
la coma, y la parte anterior al periodo; y como denominador, tantos "9"
como cifras tiene el periodo. Ejemplo:

- Decimales periódicos mixtos: Tendrá como numerador la diferencia entre
 y
y  , donde
, donde  es el número escrito sin la coma, y
es el número escrito sin la coma, y  es el número sin la parte decimal periódica, escritos ambos como
números enteros. El denominador tendrá tantos "9" como cifras tiene el
periodo y otros tantos "0" como cifras decimales no periódicas haya.
Ejemplo: Sea el número
es el número sin la parte decimal periódica, escritos ambos como
números enteros. El denominador tendrá tantos "9" como cifras tiene el
periodo y otros tantos "0" como cifras decimales no periódicas haya.
Ejemplo: Sea el número  entonces
entonces  y
y  , por lo que el número buscado será
, por lo que el número buscado será  .
.Matemáticas/Aritmética/Números irracionales
Son los números que no se pueden expresar mediante el cociente de dos números enteros y se caracterizan por poseer infinitas cifras decimales que no siguen un periodo definido.
Entre los números irracionales destacan los llamados números trascendentes. Se define un número trascendente como aquél que no es raíz de ningún polinomio (no nulo) con coeficientes enteros o racionales. Por tanto, podríamos clasificar los números reales en dos tipos: algebraicos y trascendentes.
En general, si tenemos dos cuerpos y
y  de forma que el segundo es extensión del primero, diremos que
de forma que el segundo es extensión del primero, diremos que  es trascendente sobre
es trascendente sobre  si no existe ningún polinomio
si no existe ningún polinomio ![p \in K[x]](http://upload.wikimedia.org/math/3/6/a/36a6013b43f19ae5b9eaea971cbaee30.png) del que
del que  es raíz (
es raíz (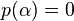 ).
).
Números reales
Es fácil de entender que todo número racional tiene una representación en forma de número decimal exacto o periódico. Dado que pueden construirse otros números en representación decimal con infinitas cifras decimales y sin periodo, éstos no son racionales. Se les denomina IRRACIONALES.
El conjunto de racionales e irracionales se denomina conjunto de NÚMEROS REALES. Se denota con la letra .
.
Números imaginarios
Los números imaginarios son aquellos que, de acuerdo a la lógica convencional, no pueden existir. Sin embargo, pueden ser el resultado de operaciones matemáticas comunes. La forma clásica de obtener un número imaginario/complejo es al obtener la raíz cuadrada de un número negativo.

Esto es debido a que, de acuerdo a lo que sabemos, los números reales elevados al cuadrado (es decir, multiplicados por sí mismos), ya sean positivos o negativos, darán como resultado un número positivo, tal como el caso de dos números positivos:
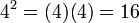
Y con el caso de dos números negativos, porque de acuerdo a las leyes de los signos, un número negativo multiplicado por un número negativo (en este caso, multiplicado por sí mismo) dará como resultado un número positivo, de forma que
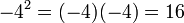
Entonces, de acuerdo a esto, no existe realmente un número tal que, multiplicado por sí mismo de como resultado un número negativo. Sin embargo podemos decir que i, la letra que representa a los números imaginarios, es igual a

Y dada esta igualdad, sería correcto afirmar que

Esto porque i equivale a la raíz cuadrada de -1, entonces, desarrollando la ecuación anterior, tenemos que

Y como ya lo sabemos, la raíz cuadrada es la operación inversa al exponente cuadrado, entonces, sabiendo que un número multiplicado por sí mismo equivale a elevarlo al cuadrado, podemos expresar esto como

Por lo tanto, también podemos decir que


Números complejos
Un número complejo es una expresión de la forma binómica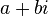 ,
donde a y b son números reales, siendo b el coeficiente de la parte
imaginaria (i). Un ejemplo de número imaginario es 4 + 2i. Los numeros
complejos junto con los imaginarios son de la clasificación de los
numeros irreales.
,
donde a y b son números reales, siendo b el coeficiente de la parte
imaginaria (i). Un ejemplo de número imaginario es 4 + 2i. Los numeros
complejos junto con los imaginarios son de la clasificación de los
numeros irreales.
Conjugado
El conjugado de un número complejo es el mismo número, pero con la parte imaginaria cambiada de signo:
 es
es  . El término real no cambia de signo.
. El término real no cambia de signo.
Clasificacion de los números complejos: Real Complejo rectangular Complejo polar.
Números reales
Es fácil de entender que todo número racional tiene una representación en forma de número decimal exacto o periódico. Dado que pueden construirse otros números en representación decimal con infinitas cifras decimales y sin periodo, éstos no son racionales. Se les denomina IRRACIONALES.
El conjunto de racionales e irracionales se denomina conjunto de NÚMEROS REALES. Se denota con la letra .
.
Introducción a las operaciones básicas
En el campo de la aritmética, cada número tiene un valor definido, así 30 siempre va a valer treinta, el símbolo del valor absoluto de un número se representa así:
 siendo n cualquier número entero, negativo o positivo
siendo n cualquier número entero, negativo o positivo
cabe resaltar que el valor de un número, esté precedido por el signo más o el signo menos, siempre será el mismo:

de esto se deduce que:

esto es porque el valor absoluto indica la distancia que hay en la recta numérica entre cualquier número y 0, y sea el número positivo o negativo, la distancia es la misma.
Como ya vimos en la clasificación de las cantidades, los Números Racionales, que serán estudiados a profundidad en este capítulo, se clasifican en ENTEROS y FRACCIONARIOS. Un número entero es, por ejemplo, 2, mientras que 0,5 ó 1⁄2 es un número fraccionario, que se puede escribir de esas dos maneras.
Números Enteros
Son aquellos números que indican una cantidad exacta. Sus operaciones básicas son, como en los otros tipos de números, suma, resta, multiplicación, división, potenciación y radicación, esta última operación se puede aplicar a un pequeño grupo de números enteros, a los cuadrados perfectos, cubos perfectos, etc.
Para sumar o restar dos números hay que tener en cuenta los signos de los mismos: para sumar dos números de iguales signos, se suman sus valores absolutos y se deja el signo que tienen; para sumar dos números con signos diferentes, se resta el valor absoluto del menor del valor absoluto del mayor y se deja el signo del mayor número.
Por ejemplo: -5-3=-8; 5+3=8; 5-3=2; -5+3=-2
La multiplicación es una suma abreviada, así 3+3+3+3+3 se puede escribir y efectuar como 3x5=15.
La división consiste en buscar un número que multiplicado por el divisor, dé como resultado el dividendo, este número buscado se llama cociente, muchas veces la división no es exacta y se obtiene un residuo. Las divisiones se pueden reprentar de las siguientes maneras:
8/2=8÷2=4, porque 4x2=8, de la misma forma: 26/13=26÷13=2, porque 2x13=26.
La poenciación es una multiplicación abreviada, consiste en dos elementos: la base, que es el factor que va a multiplicarse por sí mismo, y el exponente, que indica cuántas veces se va a multiplicar la base por sí misma: 3x3x3x3=3^4=81
La radicación, como se dijo anteriormente, es una operación que sólo puede ser aplicada a ciertos números racioneles para que el resultado siga siendo racional: si se va a aplicar raíz cuadrada, el número debe ser un cuadrado perfecto; si se va a aplicar una raíz cúbica, el número debe ser un cubo perfecto... Más adelante se explicará como se simplifican los números irracionales.
El resultado de una radicación es un número que al ser elevado al índice de la raíz, da como resultado la cantidad subradical.
√4=2; ∛27=3, cuando el índice de la raíz es 2, suele omitirse.Suma y resta de fracciones
Con el mismo denominador
Se suman o se restan los numeradores y se mantiene el denominador.



Con distinto denominador
1. Se reducen los denominadores a común denominador:1º Se determina el denominador común, que será el mínimo común múltiplo de los denominadores.2º Este denominador, común, se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.2. Se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
 m.c.m.(4, 6) = 12
m.c.m.(4, 6) = 12

Multiplicación de fracciones
El producto de dos fracciones es otra fracción que tiene:Por numerador el producto de los numeradores.Por denominador el producto de los denominadores.

División de fracciones
El cociente de dos fracciones es otra fracción que tiene:Por numerador el producto de los extremos.Por denominador el producto de los medios. .
. .
.Ejercicios de operaciones con fracciones
Una caja contiene 60 bombones. Eva se comió 1/5 de los bombones y Ana 1/2.1 ¿Cuántos bombones se comieron Eva, y Ana? 2¿Qué fracción de bombones se comieron entre las dos
2¿Qué fracción de bombones se comieron entre las dos
Un padre reparte entre sus hijos 1800 €. Al mayor le da 4/9 de esa cantidad, al mediano 1/3 y al menor el resto. ¿Qué cantidad recibió cada uno? ¿Qué fracción del dinero recibió el tercero?



Una familia ha consumido en un día de verano:Dos botellas de litro y medio de agua.4 botes de 1/3 de litro de zumo.5 limonadas de 1/4 de litro.¿Cuántos litros de líquido han bebido? Expresa el resultado con un número mixto.



Calcula las siguientes operaciones con fracciones:1
 2
2
 3
3
 4
4
 Efectúa las divisiones de fracciones:1
Efectúa las divisiones de fracciones:1
 2
2
 3
3
 Realiza las operaciones con fracciones:1
Realiza las operaciones con fracciones:1
 2
2
 Efectúa las operaciones con fracciones:
Efectúa las operaciones con fracciones:








∛(-27) buenas noches quisiera saber si este numero es racional o irracional
ResponderEliminar